type
status
date
slug
summary
tags
category
icon
password
URL
1. ODE & PDE2. Solving PDE with the power of LLM2.1 LLM PDE Solving Paradigm2.2利用LLM,获取Python 求解代码2.2.1增加”思维链”提示2.2.2 An example: LLMs for PDE solving:2.3通过调用求解器API求解PDE2.3.1 An Example(以Mathematica为例):2.4利用python interpreter执行后的结果2.5实现上的一些问题
1. ODE & PDE
常微分方程(Ordinary Differential Equations,ODE):
常微分方程是包含一个或多个未知函数及其导数的方程。在这类方程中,未知函数只有一个自变量。例如,一阶常微分方程可以写为:
其中,f(x, y)是已知函数,y是未知函数,x是自变量。这个方程表示的是y关于x的导数为f(x, y)。常微分方程在许多科学和工程领域中都有广泛的应用,例如在物理学中的牛顿运动定律,电路分析,化学反应动力学等。
偏微分方程(Partial Differential Equations,PDE):
偏微分方程是包含一个或多个未知函数及其偏导数的方程。在这类方程中,未知函数有两个或更多的自变量。例如,二维热传导方程可以写为:
其中,u是未知函数,t是时间,x和y是空间坐标,α是热传导系数。这个方程表示的是u关于t的偏导数等于α乘以u关于x和y的二阶偏导数之和。偏微分方程在许多科学和工程领域中都有广泛的应用,例如在物理学中的麦克斯韦方程,流体动力学,量子力学等。
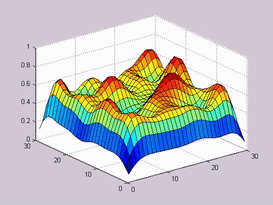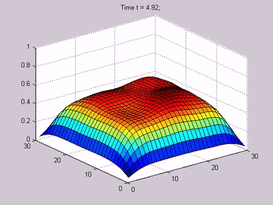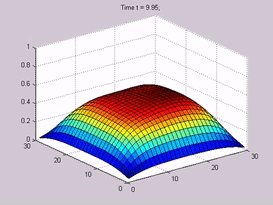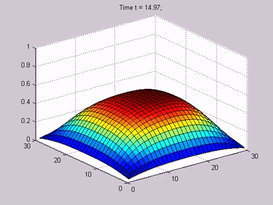
- 解偏微分方程(PDE)
- 解析方法:这些方法试图找到方程的精确解。包括分离变量法、特征值方法、格林函数法等。但是,只有对于一些特定的、形式简单的PDE,才可能找到精确的解析解。对于大多数PDE,我们无法找到精确的解析解。
- 数值方法:这些方法试图找到方程的近似解。这包括有限差分法、有限元素法、有限体积法、谱方法等。这些方法通常用于当解析方法无法应用或者不方便应用的情况。
- 求解PDE的工具:
- Python:Python有许多库可以用来解PDE,包括FEniCS、PyAMG、FiPy、SfePy等。这些库提供了一系列的数值方法,如有限元法、有限差分法、有限体积法等。
- MATLAB:MATLAB也有许多工具箱可以用来解PDE,如PDE Toolbox,提供了一系列的数值方法,包括有限元法、有限差分法等。
- Mathematica:Mathematica有强大的符号计算能力,可以用来求解一些特定的PDE的解析解。它也有数值求解PDE的功能。
- COMSOL Multiphysics:COMSOL是一款商业软件,提供了一系列的物理场模拟工具,可以用来解决各种复杂的PDE问题。
- ANSYS:ANSYS是一款广泛用于工程模拟的商业软件,它包括了一系列的模块,可以用来解决各种复杂的PDE问题。
- OpenFOAM:OpenFOAM是一款开源的流体动力学模拟软件,它可以用来解决各种复杂的流体动力学相关的PDE问题。
现存pde求解工具存在的一些问题: - 哪种工具主要取决于具体的PDE问题以及具体的应用场景, 在某些情况下,可能需要自己编写代码或者修改现有的软件,这需要一定的编程知识和对PDE求解方法的深入理解。 - 学习成本 - 方程求解成本
2. Solving PDE with the power of LLM
2.1 LLM PDE Solving Paradigm

- input:问题描述
- 求解什么样的问题
- 涉及哪些方程
- 初始条件
- 边界条件
- output:
- 解决问题的python代码
- 调用求解器api得到的求解结果
- 利用python interpreter执行后的结果
LLM 用于求解PDE的优势:
1.灵活性:大模型通常比较灵活,可以适应各种不同类型的输入数据和任务。这使得它们可以用于那些传统方法难以处理的问题,例如复杂的几何形状、复杂的边界条件等。
2.泛化能力:大模型可以具有良好的泛化能力,即可以对未见过的输入进行准确的预测,因为实际问题往往有很多未知的、难以预测的因素,这对于PDE的求解非常重要。
3.低学习成本:相较于复杂的求解软件,利用大模型可以使用偏向于自然语言的输入,将pde方程求解的问题输入给大模型,大模型将其转化为求解器能理解的语言,甚至直接利用求解器进行方程求解,最后给出求解方案或者求解结果

2.2利用LLM,获取Python 求解代码
2.2.1增加”思维链”提示
在问题输入中加入思维链提示,让LLMs来理解问题描述并将其分解为步骤,并解决每个步骤的问题。

2.2.2 An example: LLMs for PDE solving:
User Input:
我正在试图解决一维热方程,该方程形式为∂u/∂t = α*∂²u/∂x²。我设定了以下的初始条件和边界条件:
- 初始条件:在t=0时,u(x, 0) = sin(pi * x),即,热源的初始分布是一个正弦波。
- 边界条件:在x=0和x=L(L为1)处,u的值始终为0,即,u(0, t) = 0和u(1, t) = 0。
假设热传导系数α为0.01,我想要求解在t=1时刻的u(x, t)的分布。我打算使用Python和SciPy库来解决这个问题,但我不确定如何设置和解决这个问题。能否提供一个详细的Python代码示例,展示如何设置和求解这个问题?
GPT-4 Output:
你可以使用Python的SciPy库中的有限差分方法来解决这个问题。以下是一个可能的解决方案:
import numpy as np from scipy import linalg import matplotlib.pyplot as plt # 设置参数 L = 1.0 # x的范围 T = 1.0 # t的范围 alpha = 0.01 # 热传导系数 # 设置有限差分的网格点数量 Nx = 50 # x方向的网格点数量 Nt = 50 # t方向的网格点数量 # 计算每个方向的步长 dx = L / (Nx - 1) # x方向的步长 dt = T / (Nt - 1) # t方向的步长 # 创建网格点坐标 x = np.linspace(0, L, Nx) # x方向的网格点坐标 t = np.linspace(0, T, Nt) # t方向的网格点坐标 # 创建用于保存解的数组 U = np.zeros((Nx, Nt)) # 设置初始条件 U[:, 0] = np.sin(np.pi * x) # 设置边界条件 U[0, :] = 0 U[-1, :] = 0 # 创建用于离散化方程的矩阵 A = np.eye(Nx-2) * (1 + 2 * alpha * dt / dx**2) A += np.diag(-alpha * dt / dx**2 * np.ones(Nx-3), k=-1) A += np.diag(-alpha * dt / dx**2 * np.ones(Nx-3), k=1) # 使用有限差分法进行迭代 for j in range(Nt-1): U[1:-1, j+1] = linalg.solve(A, U[1:-1, j]) # 绘制结果 plt.imshow(U, extent=[0, T, 0, L], origin='lower') plt.colorbar(label='u(x,t)') plt.xlabel('t') plt.ylabel('x') plt.show()
这个代码首先设置了问题的参数,然后设置了有限差分的网格点数量。然后,它创建了网格点坐标,并设置了初始条件和边界条件。接着,它创建了用于离散化方程的矩阵,并使用有限差分法进行了迭代。最后,它绘制了结果。
注意,这个代码使用了显式的有限差分方法,这意味着它可能对时间步长和空间步长的选择比较敏感。如果你发现解不稳定,你可能需要减小时间步长或增大空间步长。
Code execution result:

2.3通过调用求解器API求解PDE
除了python库,还有很多软件具有求解PDE方程的能力:
- Wolfram Mathematica(Wolfram Alpha)
- ANSYS Fluent
- OpenFoam
此时大模型需要将用户输入的自然语言求解问题翻译为求解器能够理解(使用)的语言,并通过某种方式调用求解器
2.3.1 An Example(以Mathematica为例):
用户输入一个热学偏微分方程求解问题:
我正在试图解决一维热方程,该方程形式为∂u/∂t = α*∂²u/∂x²。我设定了以下的初始条件和边界条件:
- 初始条件:在t=0时,u(x, 0) = sin(pi * x),即,热源的初始分布是一个正弦波。
- 边界条件:在x=0和x=L(L为1)处,u的值始终为0,即,u(0, t) = 0和u(1, t) = 0。
假设热传导系数α为0.01,我想要求解在t=1时刻的u(x, t)的分布。我打算使用Python和SciPy库来解决这个问题,但我不确定如何设置和解决这个问题。能否提供一个详细的Python代码示例,展示如何设置和求解这个问题?
LLM 需要将自然语言翻译为Mathematica语言
此后求解任务转换到求解器身上(如Mathematica/Wolfram Alpha)
求解器求解后,将结果返回给系统,系统再展示求解结果
2.4利用python interpreter执行后的结果
Open-source GPT-4 Code Interpreter
类似于GPT-4 Code Interpreter,只不过此时仅通过langchain中的PAL-chain调用Python REPL 实现Python code 解释器的功能

PAL实现了自然语言到代码的转换, 将数学问题转换成了可执行python代码
REPL
Chain of Thought利用了大模型多部推理的能力,但是一些时候大模型甚至会在一些加减法处理上犯致命错误。
PAL弥补了这一点,PAL同样利用了CoT将复杂问题进行拆分的思想,但是在执行上采用了python interpreter,进一步提升了大语言模型解决复杂数学问题的能力
A simple PAL demo with langchain
from langchain_experimental.pal_chain import PALChain from langchain import OpenAI llm = OpenAI(temperature=0, max_tokens=512) pal_chain = PALChain.from_math_prompt(llm, verbose=True) question = """ Jan has three times the number of pets as Marcia. Marcia has two more pets than Cindy. If Cindy has four pets, how many total pets do the three have? """ pal_chain.run(question)
> Entering new PALChain chain... def solution(): """Jan has three times the number of pets as Marcia. Marcia has two more pets than Cindy. If Cindy has four pets, how many total pets do the three have?""" cindy_pets = 4 marcia_pets = cindy_pets + 2 jan_pets = marcia_pets * 3 total_pets = cindy_pets + marcia_pets + jan_pets result = total_pets return result > Finished chain. '28'

2.5实现上的一些问题
- zero shot:对于现有的很多大模型,尤其是GPT-4,在CoT的加持下,对于一些简单的pde方程求解问题,已经可以用其生成效果较为不错的python代码或者求解器语言
- pal:pal实现了部分GPT-4 Interpreter功能,但是目前效果在于求解一些简单或者中等的数学问题上表现较好,如果想借用其思路实现PDE求解还需要进行进一步完善
- fine-tuning:为了更好的求解pde,fine-tuning是很有必要的,目前的大模型方向是通用大模型,除了GPT-4这样的六边形战士有着较好的表现,其他开源模型在pde python代码生成方面表现还不是很好
- 一些代码生成大模型表现怎么样:清华CodeGeeX2 对于pde求解的代码生成目前还很乏力,其更多的适用于部分代码补全, Copilot,CODEX (code-davinci-002)等还待测试
- Example
- baseline
- 时间
- 1d→2d
- 作者:GTX
- 链接:https://blog.gongtx.org/article/0255dd76-96d8-418a-b094-ed57068d7964
- 声明:本文采用 CC BY-NC-SA 4.0 许可协议,转载请注明出处。
相关文章
2023-11-03
Woodpecker: Hallucination Correction for Multimodal Large Language Models
2023-10-25
Automatically Correcting Large Language Models: Surveying the landscape of diverse self-correction strategies
2023-09-06
Review of Agentbench
2023-09-01
Review of Learning to Retrieve In-Context Examples for Large Language Models
2023-08-25
Review of WizardLM
2023-08-06
Review of ScienceQA





